Working in the UW-Madison Physics Department, I developed new methods for extracting information from optical atomic clock comparisons. The project focused on improving the precision of quantum state estimation using machine learning and statistical approaches. Below is a summary of the work I did.
Thesis Summary
This thesis explores two machine learning methods for fitting elliptical data from atomic clock experiments: a neural network and a maximum likelihood estimate (MLE). These methods aim to improve the accuracy of phase extraction compared to the existing least-squares (LS) method.
Background
Atomic clocks are crucial for GPS, telecommunications, and scientific research. Improved timekeeping can enhance GPS accuracy, enable earthquake prediction, and aid in studying dark matter. Some atomic clock experiments produce elliptical data, and fitting this data accurately is essential for extracting phase differences that reveal environmental conditions.
The study focused on the Multiplexed Optical Lattice Clock, which uses ensembles of strontium atoms cooled near absolute zero. Observing phase shifts between these ensembles helps measure gravitational redshift at sub-centimeter scales.
Methods
1. Least-Squares Algorithm
- Current standard: Fits elliptical data but is biased, especially with noise or certain phase values.
- Bias correction: Applied a tangent-based regression fit to correct phase bias.
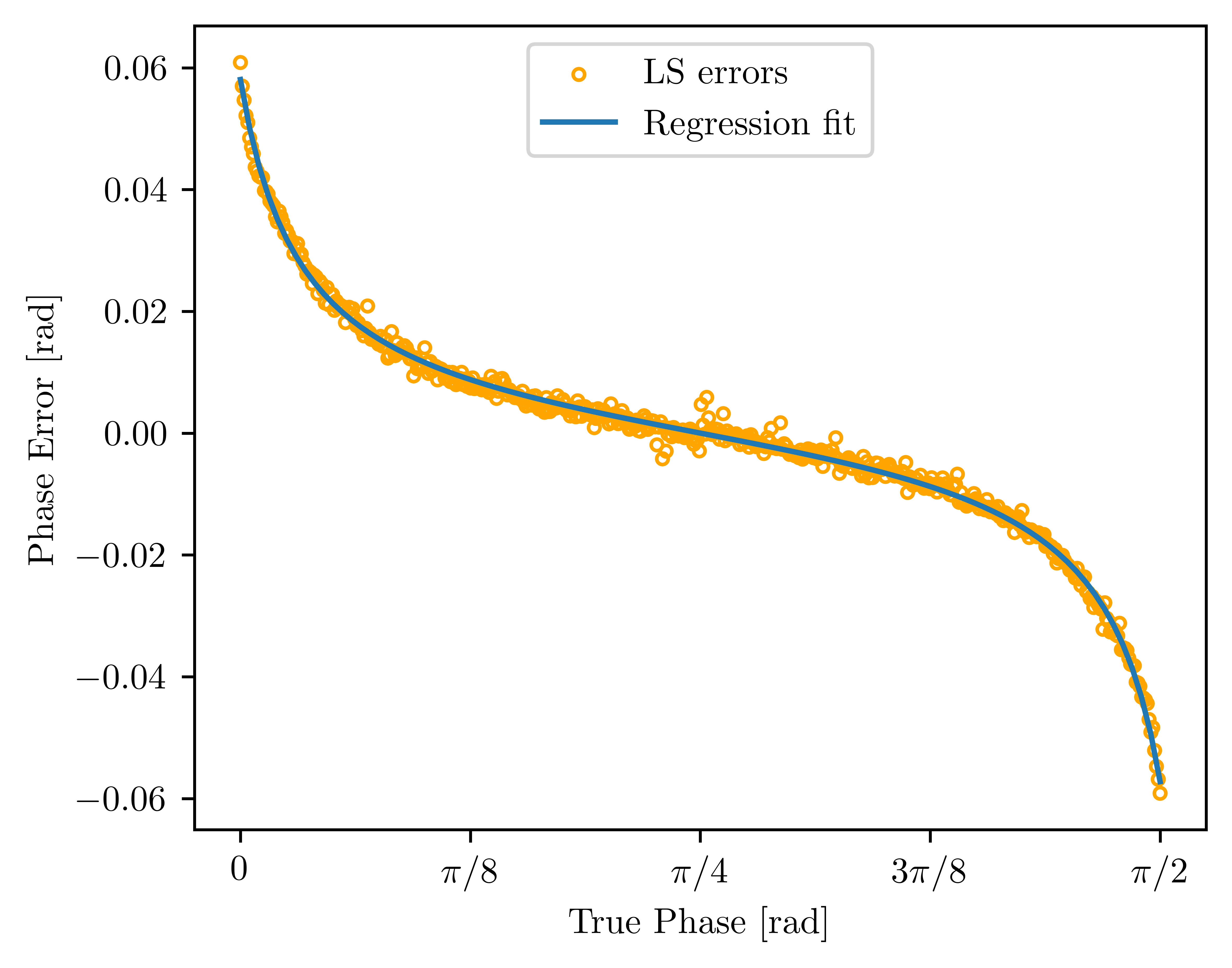Least-squares phase bias showing overestimation at phase 0 and underestimation at phase π/2.
2. Neural Network
- Training data: Generated using Monte-Carlo simulations with quantum projection noise.
- Architecture: Input layer for up to 500 points, ReLU activation, and MSE loss function.
- Hyperparameter tuning: Conducted via Weights & Biases platform, training 2489 models.
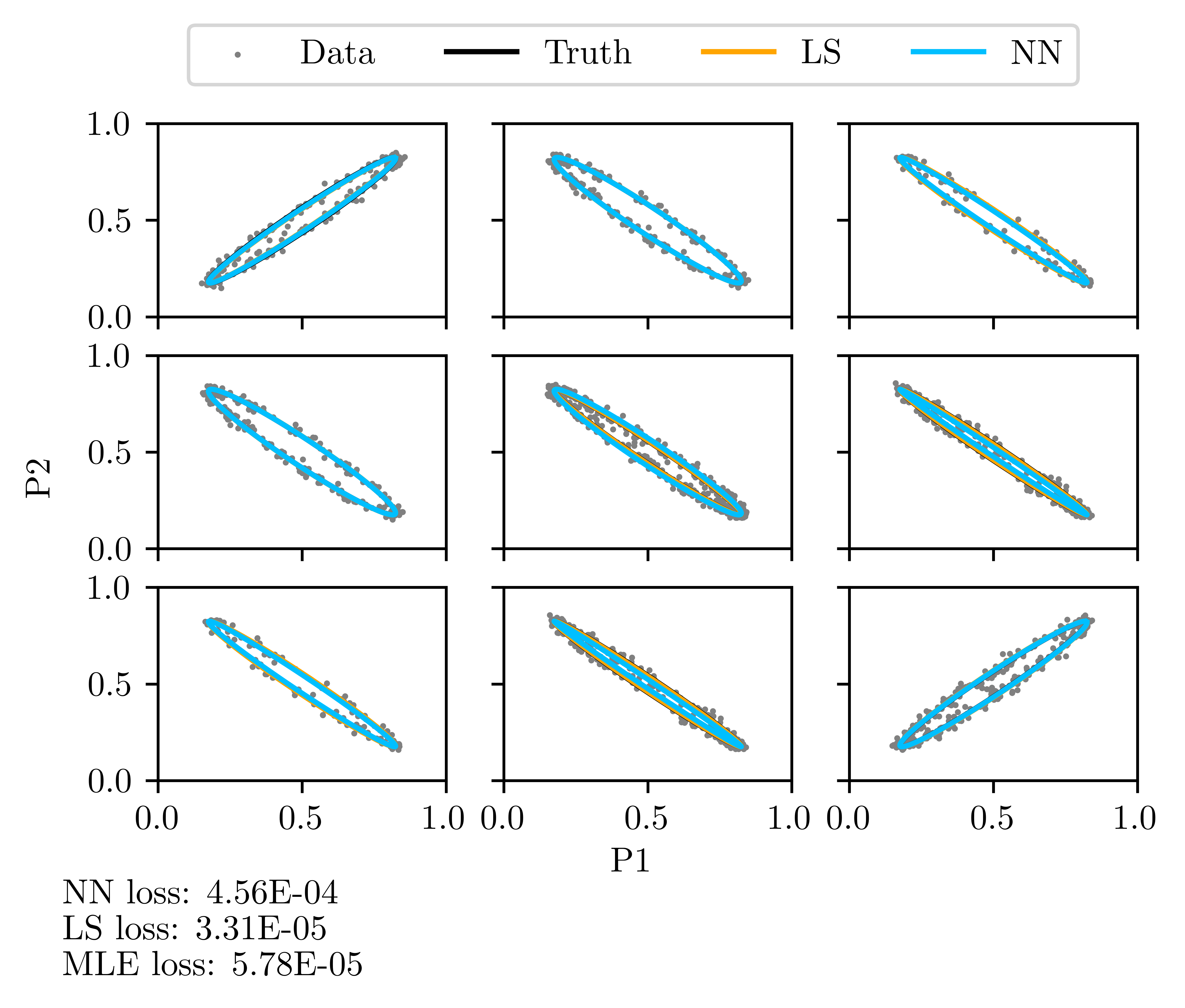Initial neural network fits for elliptical data with and without noise.
3. Maximum Likelihood Estimate
- Method: Optimizes phase and contrast parameters by maximizing likelihood using bivariate Gaussian approximations.
- Bias assessment: Showed no phase bias, unlike LS.
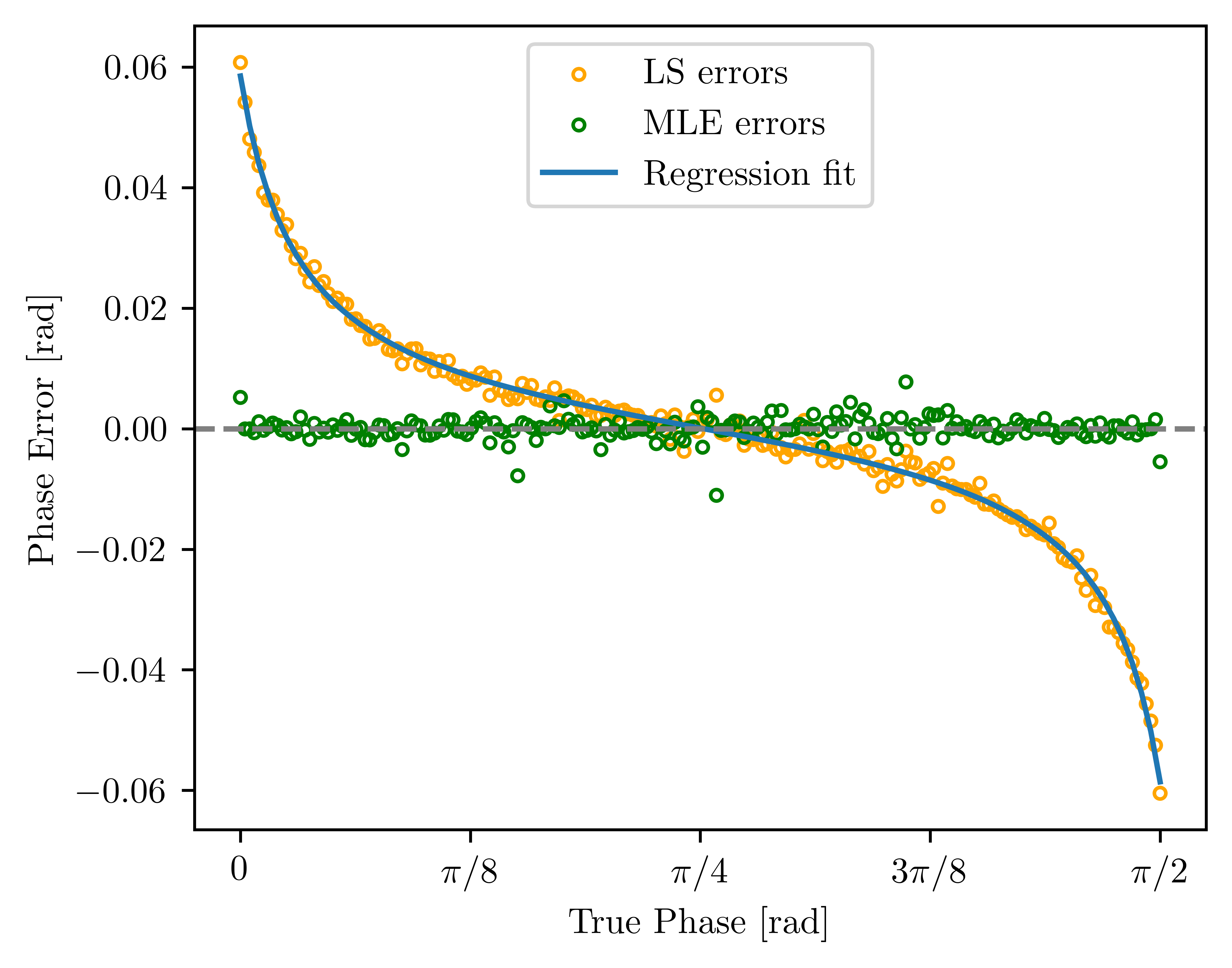MLE phase errors demonstrating consistent accuracy across all phases.
Results & Performance
| Method | MSE Loss | Bias | Performance |
|---|---|---|---|
| Least-Squares | Low (corrected) | High (uncorrected) | Best with few points, sensitive to noise |
| Neural Network | Higher than LS and MLE | Low | Underperformed LS despite extensive training |
| MLE | Comparable to LS | Low | Outperformed LS with many points or high noise |
Comparison of MLE and LS algorithms across different data complexities.
Conclusion
- LS Algorithm: Remains the most reliable for small datasets.
- Neural Network: Promising but needs further tuning.
- MLE: Best suited for large datasets or noisy environments.
This work demonstrates that MLE provides a robust alternative to LS for atomic clock experiments, paving the way for more precise timekeeping and technological advancements.